Storage
Storing positive numbers
A 1 bit number can store two numbers {0, 1}, 2-bit number can store 4
{0,1,2,3 => 00,01,10,11} and so on.
A n-bit number stores numbers 0 to \(2^n-1\).
Below is a function to compute the number of bits needed to store positive numbers up to a specific
number.
import math
def infer_num_bits_pos(num: int) -> int:
"""Number of bits needed to store 0 to positive numbers upto ``num``.
Sample input and output::
num = 3
output = 2
num = 4
output = 3
"""
if num <= 1: return 1
nbits_pos = math.log2(num)
if nbits_pos.is_integer():
# Multiple of 2
# For exact multiples of 2, we need one more bit. For example 8 = 2^3 => 1000.
return int(nbits_pos) + 1
else:
return math.ceil(nbits_pos)
def infer_num_bits_pos_2(num: int) -> int:
"""Number of bits needed to store positive numbers."""
if num == 0:
return 1
n = 0
while num:
num = num >> 1
n += 1
return n
Storing integers (negative, 0 and positive)
However, we don’t have to restrict ourselves to non negative integers. Say we want to store
-4 to 3, we have eight numbers, so a 3-bit store should be able to support this.
A n-bit number stores numbers \(-2^{(n-1)}\) to \(+2^{(n-1)} - 1\).
The reason we can store one fewer positive number is because we need to also represent 0.
Example: 2-bits can store -2 to 1, 3-bits can store -4 to 3, 4-bits can store -8 to 7 and so on.
We store negative integers in 2s-complement form. The most significant bit (MSB) is
a sign bit that is 0 if non-negative and 1 if negative. The negative of a number is the number
that needs to be added to the positive binary representation of the number to produce the
number \(2^{\text{num-bits}}\). This can be obtained adding 1 to the not of the
positive number. This technique works if you want to convert a negative number to positive
as well.
def flip_sign(num):
return ~num + 1
Example 1: Let’s use a 4-bit number. The numbers that can be represented here are -8 to 7. Say we would like to find the 2s complement representation of -6.
6 => 0 110 (MSB is the sign bit)
~6 => 001 + 1
=> 010
-6 => 1 010
Example 2:
Let’s use a 8-bit number. The numbers that can be represented here are -128 to 127. Say
we would like to find the 2s complement representation of
-123
# This will be 127-7 ones, minus 4, 100.
# 2^7 is 128, for which we need 8 bits 1000_0000, so 0111_1111 will be 127.
123 => 0 111_1011
~123 => 000_0100 + 1
-123 => 1 000_0101
-32
# 2^5 (so needs 6 bits)
32 => 0 010_0000
~32 => 101_1111 + 1
-32 => 1 110_0000
-64
# 2^6 (so needs 7 bits)
64 => 0 100_0000
~64 => 011_1111 + 1
=> 100_0000
-64 => 1 100_0000
From above the pattern is clear, the negative integers which are powers of two are represented as ones followed by zeros.
-128. We actually need 8 unsigned bits to represent +128, 1000_0000. If we do a negation
0111_1111 and add 1. We get 1000_0000. That is all the 7 unsigned bits are 0. We allow
the carry over to fall through and set the MSB to 1 to mark negative. So as you would
expect, in a signed context -128 will be 1000_0000.
def infer_num_bits_integers(num: int) -> int:
"""Number of bits needed to store negative, 0 and positive numbers with
absolute value is at least up to ``num``.
Sample input and output::
3 => -2^2 to 2^2-1 => 3 bits
-4 => -2^2 to 2^2-1 => 3 bits
5 => -2^3 to 2^3-1 => 4 bits
8 => -2^4 to 2^4-1 => 5 bits # special case
"""
if num == 0: return 2
nbits = ceil_log2(abs(num))
if nbits.is_integer() and num > 0:
# For exact positive multiples of 2, we need one extra bit. This is not true for
# negative multiples of 2. With 5 bits, we can store numbers between -16 to 15, ie.,
# -2^4 to (2^4 - 1). `34
return int(nbits) + 2
else:
return math.ceil(nbits) + 1
Finding the rightmost set bit (rightmost 1)
Something you can notice above in the two’s complement representation is that x and -x only have one common set bit which is the rightmost bit. Also for powers of two there’s exactly one set bit.
So for the leetcode problem find if a number is a power of 2, you can simply do
if n == 0:
return False
else:
return (x & (-x)) == x
Shifting
>>> x =0
>>> x = x | 1 << 4
>>> x
16
- Left shifting 1 by n is the same as raising 2 to the power of n.
- If you left shift by n, the output is a (n+1)-bit binary. For example if you left shift by 1, the output is a 2-bit binary number (2 => 10). Another example \(2^6\) is a 7-bit binary number.
- Left shifting a number n times is the same as multiplying the by \(2^n\).
- Right shifting a number n times is the same as dividing the by \(2^n\).
In [1]: a = 25
In [2]: a >> 3
Out[2]: 3
In [3]: a << 2
Out[3]: 100
Masking
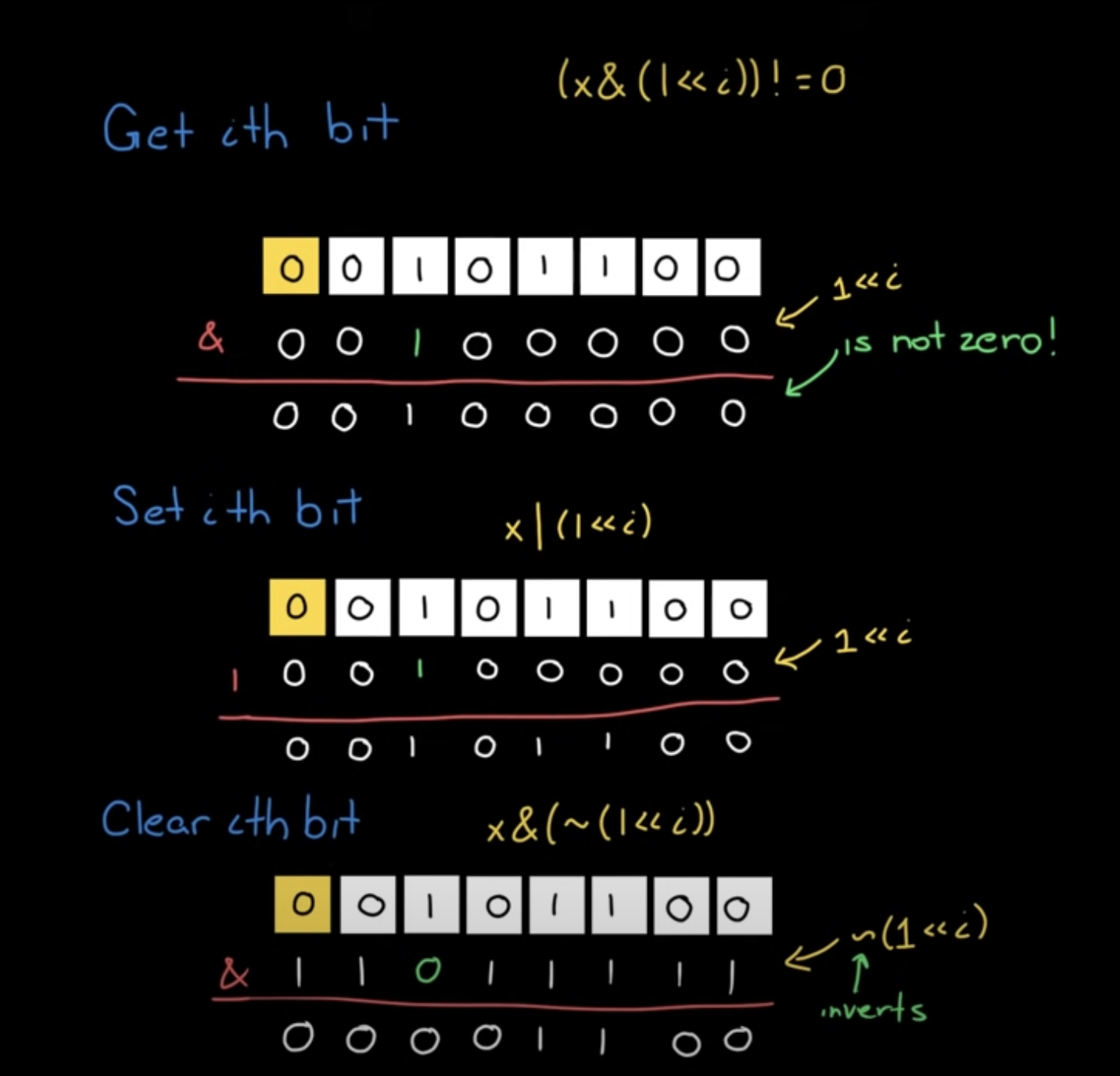
Bits are indexed 0 to n-1. So a 8-bit number is indexed 0 for the LSB and 7 for the MSB.
Credits: Picture below from hackerrank tutorials.
For below remember i begins at 0.
- Checking if
i-thbit is set:x & (1 << i) - Setting the
i-thbit (setting it to1):x | (1 << i) - Clearing the
i-thebit (setting it to0):x & (~(1 << i))
Make python understand that MSB is sign-bit
# if num is 32 bit int, largest possible value is 2^31 - 1
if lone >= (1 << 31):
lone = lone - (1 << 32)