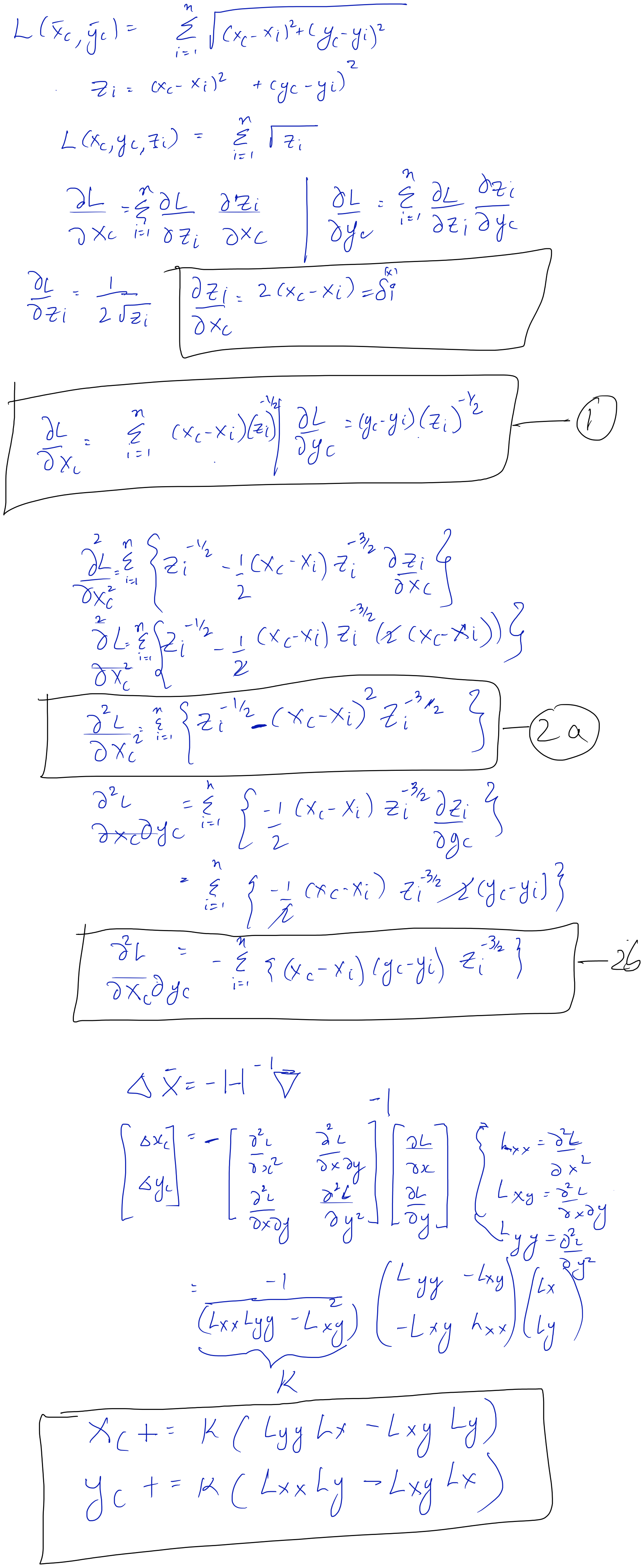Home


Challenging problems

Last updated: 27 January 2023


Table of Contents

  1. Monotonic stack problems
  2. Gradient descent, Newton’s Method: Leetcode #1515

Monotonic stack problems

Examples of such problems

In these problems we are given a list of numbers (int/float) and for each element in this list, we need to know the largest subarray that includes this number such that this number is either the greatest or the smallest in the subarray.

In the Largest rectange in histogram problem, for every element we need to know the largest subarray such that the element is the smallest number in the subarray. In other words we need to know how far can we expand on each side of an element so that all the elements in the subarray are at least this number. These problems can be trivially solved in \(O(n^2)\), by building all possible subarrays. However all of these problems can be solved in \(O(n)\) time using a monotonic stack.

For input nums of length n, The solution approach that I like is to create 3 datastructres.

  • left list of length n: Each element left[i] contains the index of the nearest element to the left of in nums[i] such that nums[left[i]] is smaller or greater than nums[i]. If we want to keep the invariant that nums[left[i]+1:i+1] are at most nums[i], then left[i] will contain the index of the nearest element to the left of nums[i] that is greater than nums[i].
  • right list of length n: The same but from the right of the array.
  • Monotonic Stack stk: Used in the intermediate calculations to build left and right. The stack contains the StackItem(index, val). If we want to build left[i] or right[i] such that they store the nearest number greater than nums[i] on either side, then we keep the invariant that the largest number is at the bottom of the stack and the smallest number is on the top of the stack. Any time we get a new nums[i] such that nums[i] is greater than or equal to the top of the stack, keep popping from the stack until you find the first number greater than this number, it’s index will left[i] or right[i]. If you find a number that is smaller than the top of the stack then left[i] will simply the be the index of the element on the top of the stack (because first number larger this number) and we push the current number into the stack.
from collections import deque
import dataclasses


@dataclasses.dataclass
class StackItem:
       ix: int
       val: int


class Solution:
    def maxSumMinProduct(self, nums: List[int]) -> int:
        if not nums:
            return 0
        left_ixes, right_ixes = build_lt_rt_indices(nums)
        ps = build_prefix_sum(nums)
        max_smp = 0
        for lt, rt, num in zip(left_ixes, right_ixes, nums):
            # If there is no number smaller than num to the left of num, then the sum
            # of the array should simply the prefix_sum[rt-1]. rt-1 because
            # nums[rt] < num.
            lt_ps = 0 if lt == -1 else ps[lt]
            max_smp = max(max_smp, (ps[rt-1]-lt_ps) * num)
        return max_smp % (10**9 + 7)


def build_lt_rt_indices(nums):
    n = len(nums)
    # Stores the index of the nearest number to the left and the right that is
    # smaller than this number.
    left, right = [None] * n, [None] * n
    # Build left indices
    stk = deque([StackItem(ix=-1, val=-float('inf'))])
    for i, num in enumerate(nums):
        while stk[-1].val >= num:
            stk.pop()
        left[i] = stk[-1].ix
        stk.append(StackItem(ix=i, val=num))
    # Build right indices
    stk = deque([StackItem(ix=n,val=-float('inf'))])
    for i, num in reversed(list(enumerate(nums))):
        while stk[-1].val >= num:
            stk.pop()
        right[i] = stk[-1].ix
        stk.append(StackItem(ix=i, val=num))
    return left, right


def build_prefix_sum(nums):
    prefix_sum = [None] * len(nums)
    rs = 0
    for ix, num in enumerate(nums):
        rs += num
        prefix_sum[ix] = rs
    return prefix_sum


Gradient descent, Newton’s Method: Leetcode #1515

Best Position for a Service Centre

In this problem we are given a list of positions with x, y coordinates. We need to find the point that has the least euclidean distance to all the points. Using vanilla gradient descent solves most test cases. However, to solve all the test cases within the prescibed time we need to use

  • Second order approximation with Newton’s Method for the first 1000 steps.
  • Gradient descent with a clever learning rate decay schedule.
  • Momentum while computing the gradients and hessian.
  • And early stopping by comparing the average losses in the last 1000, to the previous 1000 steps.

Github Solution

Given below is the derivation for the step update using the second order approximation or Newton’s method by computing the Hessian.