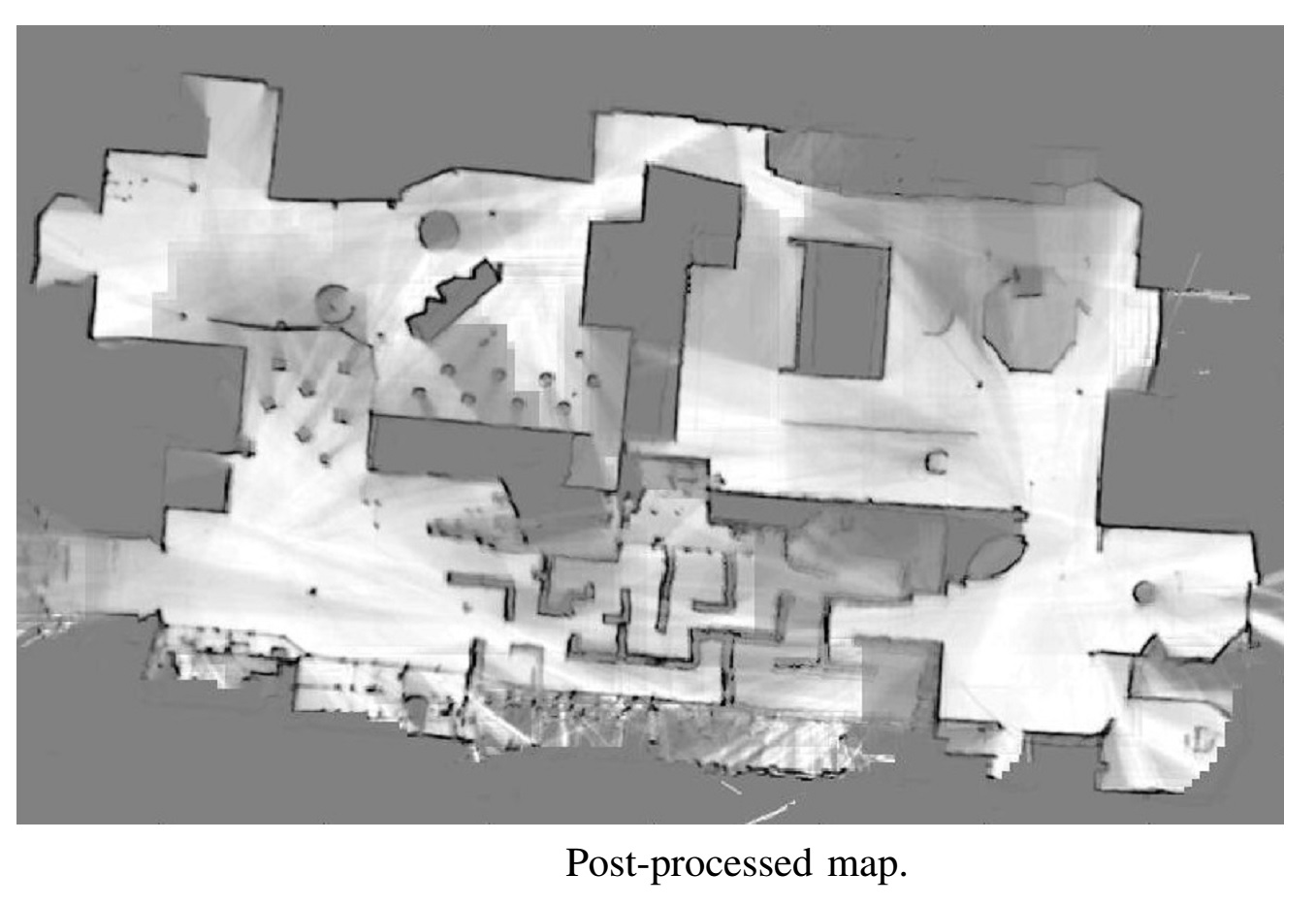
Multi-robot map merging with Graph-SLAM Posted on August, 25th, 2014
Abstract
Mapping large environments using mobile ground based robots is
becoming increasingly popular with the recent improvements in the
efficiency and accuracy of realtime Simulatenous Localizatin and
Mapping (SLAM) algorithms. In most situations it is lucrative to
have multiple robots simultaneously map different regions of the
environment for faster exploration. The most popular algorithm for
merging the individual maps is the Bundle Adjustment (BA) or the
landmark based GraphSLAM. In this project I use a simplified offline
GraphSLAM algorithm for merging the individual 2D maps generated by
any number of robots. The robots are assumed to have implemented
some form of SLAM so that in a small region the maps generated are
accurate. I utilize scan matching with LIDAR sensors and replacing
landmark features in the BA algorithm with smaller sub maps of the
map created by each robot. The optimization problem is formulated as
a least square error minimization by employing a graph structure.
The optimization in this paper is performed into two parts: (1) the
correction of the heading angle followed by (2) the correction of
the X and Y positions of the local maps. The results show that
though the problem is quadratic in time in the total number of
smaller sub maps, it produces robust results and therefore is a very
attractive option.
Methodology
-
Merge all the individual robot maps to create a dead reckoning
map.
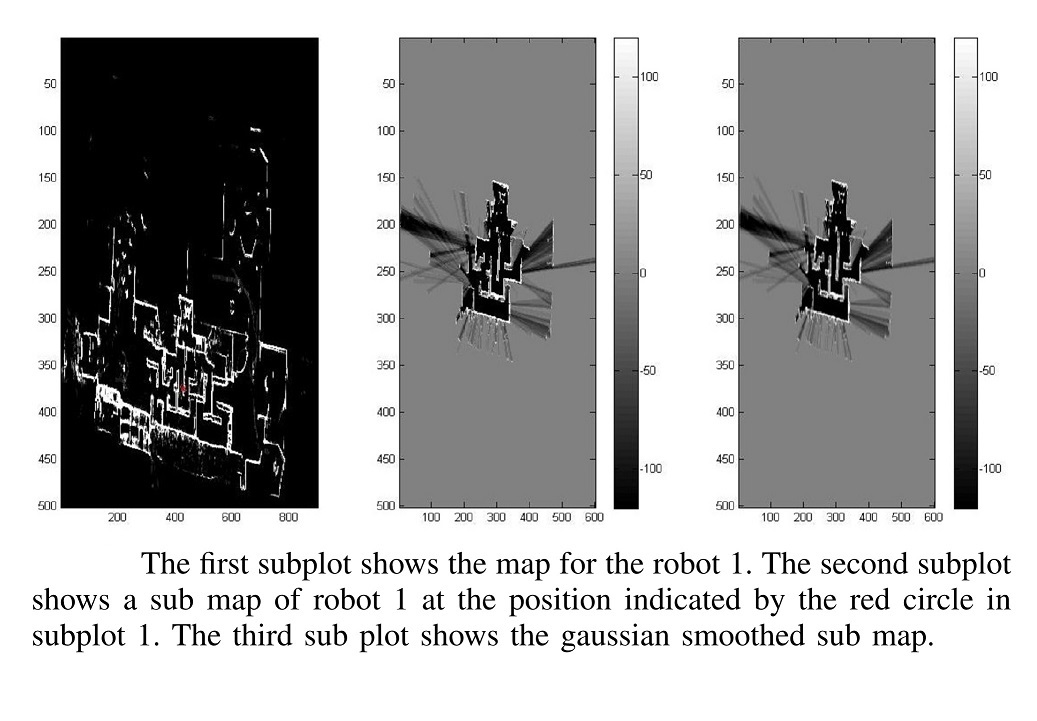
-
Combine pose positions together to create submaps for each
robot.
Problem definition
The dataset used in this project was obtained from the General Robotics, Automation, Sensing and Perception Lab (GRASP) team of the University of Pennylvania from the data collected in their participation in the Magic 2010 challenge. The competition required the participants to design and deploy a team of field robots that could explore and map a large dynamic urban environment while simultaneously localizing, identifying and responding to threats in the environment. The data is obtained from five robots exploring different regions of the environment with a fair amount of overlap in the regions explored. This enables merging of the maps using loop-closures (when the robots comes back to the same position it has or another robot has been before). The robots are equipped with a vertical and a horizontal lidar sensor, an IMU and a GPS tracking system. The robots performed a highly optimized scan matching technique for SLAM, to build a probabilistic grid map. The data provided include the poses of the robots in the global reference frame including their x,y positions and the yaw, pitch and roll angles. Also included is the horizontal and the vertical LIDAR hits in the global reference frame, along with a specification of which LIDAR hit corresponds to an obstacle. This obstacle information is important especially in the case of the vertical LIDAR. This information could be used to find ditches or pits which could otherwise be confused with obstacles. The GPS information provided has a low resolution and could not be used in the SLAM algorithm with any suitable benefits. For the purposes of this project we are only interested in the x,y positions and the LIDAR data, other informations are irrelevant.-
Try to find if the same part of the map (or close to the same
region)is revisited by comparing the submaps. Find the peak hough
angles for each submap and rotate each pair of submap through the
peak hough angles and find the scan matching. If the maximum is
above a threshold accept as a loop closure and use the shift from
the center in scan matching as a virtual measurement which should
correct the initial pose estimates assumed as odometry.
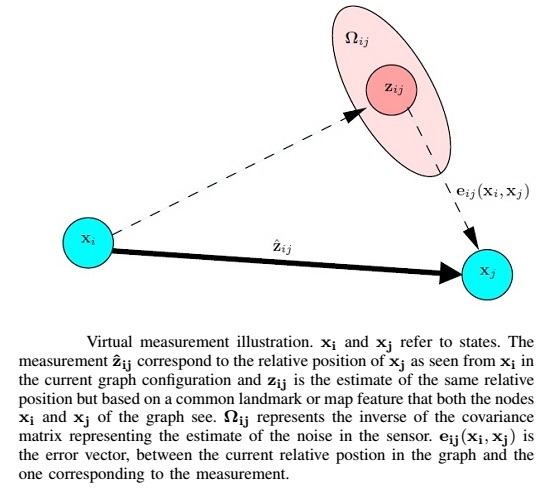
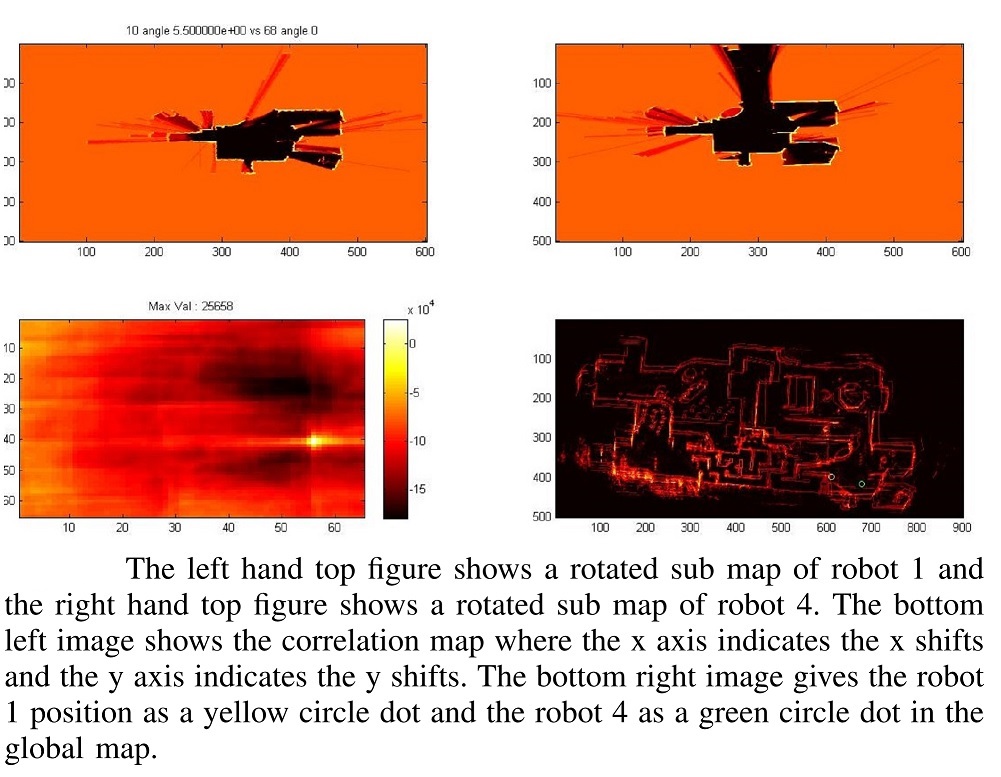
-
Find all the matches in the submaps and plot the graph connections
to build the information matrix and the information vector for the
angle alone.
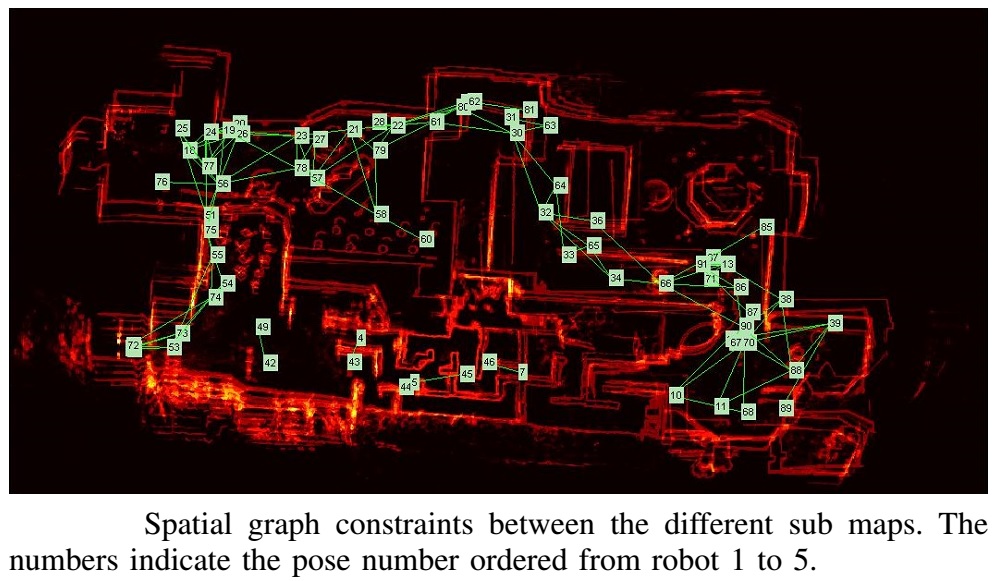
-
Now solve the least squares to get all the submaps to the right
rotated angles. We can fix the x,y later. This avoids bringing the
difficulty of building a covariance matrix which is dependant on
x,y and the rotation angle, and making only a variance for the
angle.
-
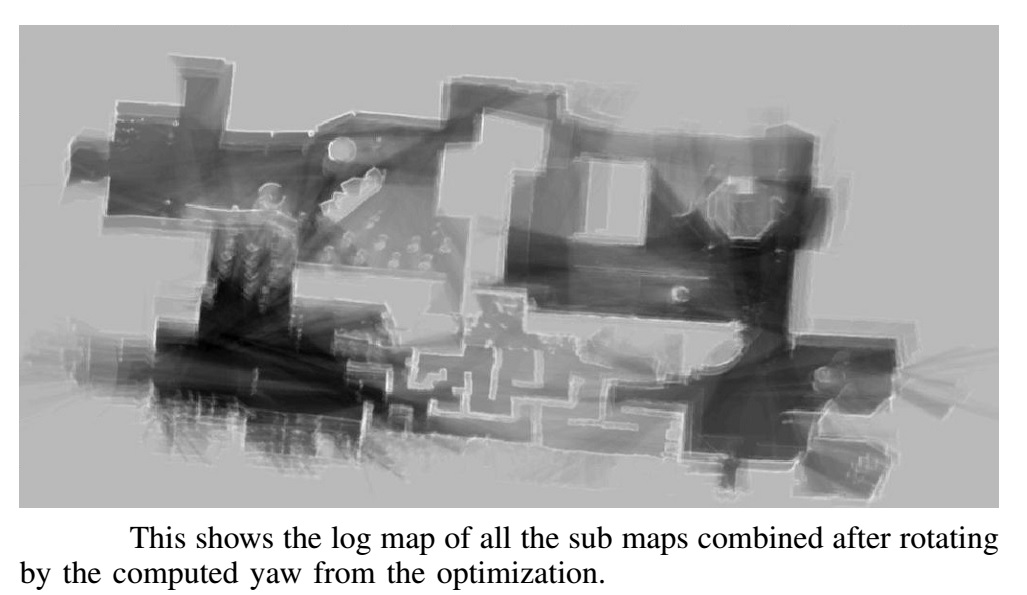
Now with the corrected graph and submaps build the information
matrix and the information vector for the x,y positions with the
covariance matrix. And solve the least square problem to solve the
map merging problem and the final log probability map. Do some
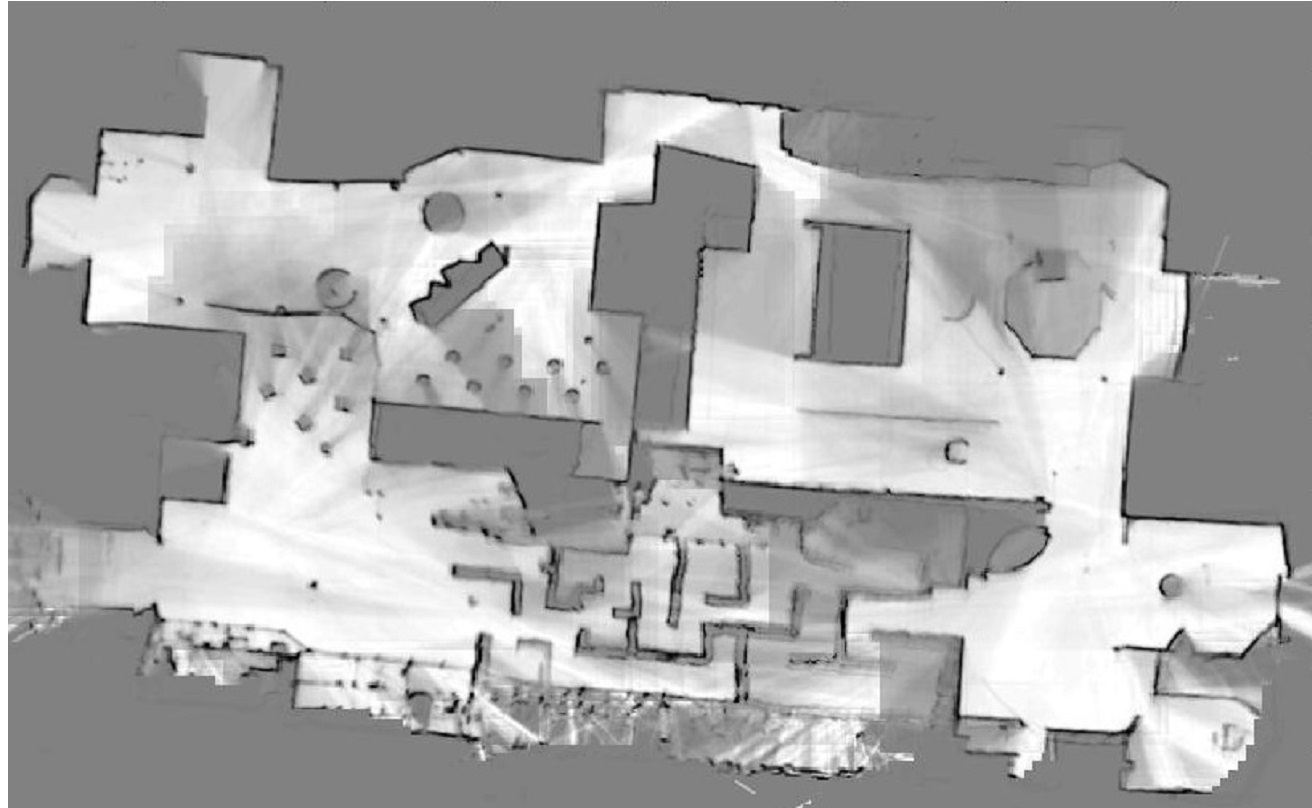
post processing to make the map look better.